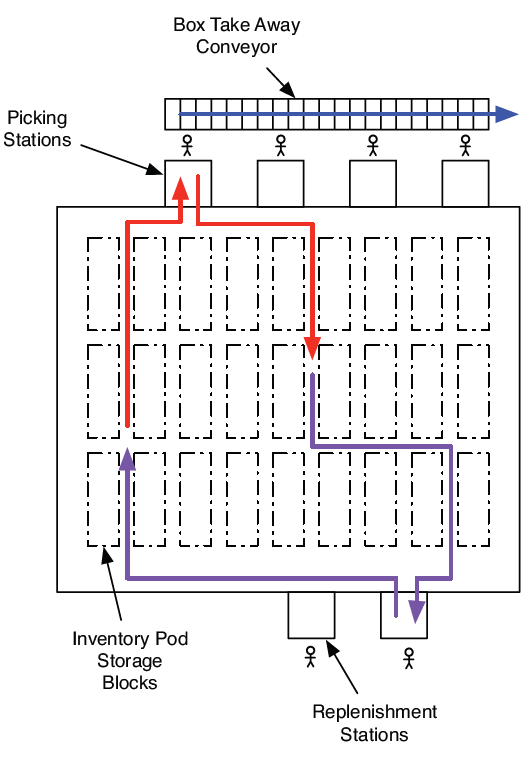
Concretely, PMOG is applicable in robotic warehousing systems: the pebbles represent robots that access physical locations. This example is not as far fetched as it sounds: thousands of robots are delivering packages from storage to packing stations in warehouses every day and Kiva Systems is the company that pioneered their use, before being acquired by Amazon in 2012. It’s also not new: Staples was the first company to go live with a Kiva system in 2006! A 2016 report estimated that Amazon was operating ~30k units and by 2022 Amazon reported 520,000 world-wide. The next two images show the layout of a typical robotic distribution center and the robots they employ. Robots pick up and deliver shelves of inventory to pick/pack workers. See the image source for more information.

Let robots find their way using something like A*, if another robot gets in the way, simply wait until the node is free again. Using the Alphabet Soup multi-robot simulator, I modified the default behaviour to strictly adhere to the underlying navigation graph. Then, I only allowed robots to enter a node if it is empty. The next video shows what it looks like: the robots are pink, replenishing stations are blue, shelves are purple and packing stations are green. In this simulator, the shelves contain letters and the parcels being packed are words from a dictionary.

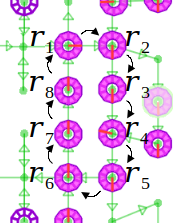
Let’s focus on a single stuck robot and assume it can order others to move out of its way. A Breadth First Search (BFS) for the first open node reveals the shortest path of moves to clear the blocked node (i.e the ‘swap path’). The process is shown in the following animation. In some cases, robots start in their target positions, or reach them by moving out of the way for others, this is a fortunate accident.

The next video shows a simulator I wrote in Java to develop the deadlock resolution strategy. Square brackets represent grid positions and numbers represent robots. Each node is the target of the robot with the same number and the grid is numbered in row major order, meaning if every robot were in its destination position, it would look like this:

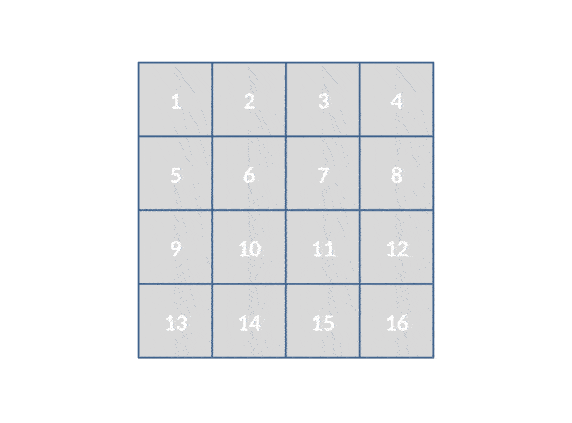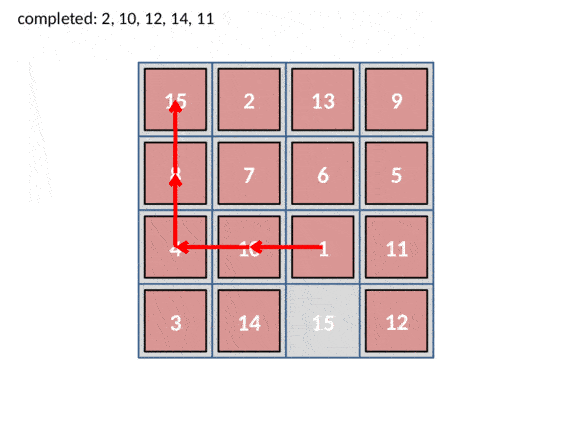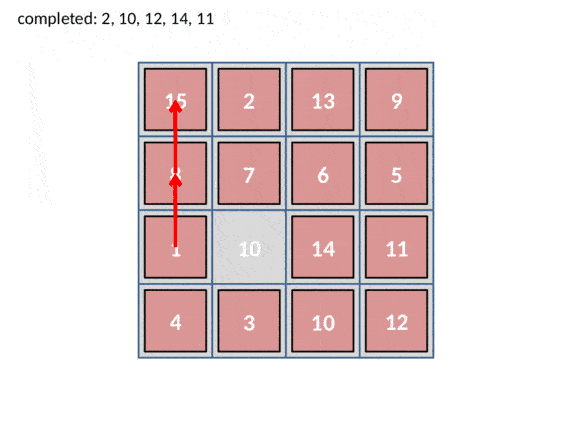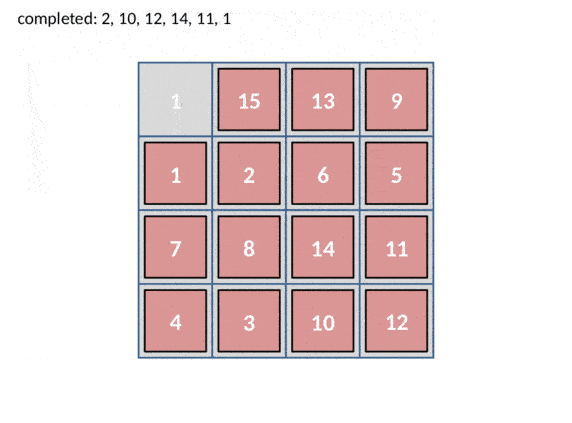
The previously described process is repeated for every robot. The robot currently in control of all moves is indicated as ‘Moving pebble’ and all unfinished robots are shown in the ‘Pebbles queue’. The pebbles queue determines which robot gains control next and was populated randomly, since the order doesn’t matter. As expected, all robots eventually end up in ‘Completed’.

Simultaneous motion is achieved by assigning a priority to each robot and defining a round consisting of two phases. In a first phase, robots instruct each other to move along the swap path determined using BFS. A robot sends instructions either to itself or the robot at the tip of the swap path. Robots send instructions to themselves in two scenarios: 1) to move to the next node, and 2) to remain in place while ordering others to move. This ensures that high priority robots decrease their distance from their target monotonically, which in turn ensures that progress is being made. Idle robots don’t send instructions but receive them. At the end of this phase, each robot selects the highest priority instruction and forwards it as a node access request, maintaining the original sender’s priority.

In the second phase, nodes select the highest priority request to notify successful requesters and these robots move. Then, all robots empty their instruction queues. This ends the round and the process repeats until all tasks are complete, at which point no one sends instructions and everything stops. In the next video, the same task assignments are used as before. Lower numbers mean higher priorities, making life hard for robot 10!

Getting the details (available in my thesis) right is really difficult. Instead of slogging through that, let’s see it in action! In the next videos, robots indicate completion by highlighting themselves in red and indicate node visits by marking them with a purple circle. These robots have randomly initialized acceleration and speed limits to simulate real-world variances. The first video has tasks assigned in row-major order, however, any task assignment is allowed. In fact, robots can even all have the same target node as shown in the second video which is an example of an assignment that is infeasible in PMOG.

So far only single tasks were assigned. Multiple tasks can be assigned by setting each robot’s priority equal to their task number. Even if one task is delayed by many others, as overriding tasks complete, the blocked task’s priority effectively raises until it overrides every other robot. The video below shows robots cyclically completing multiple random node visits without marking their destinations.

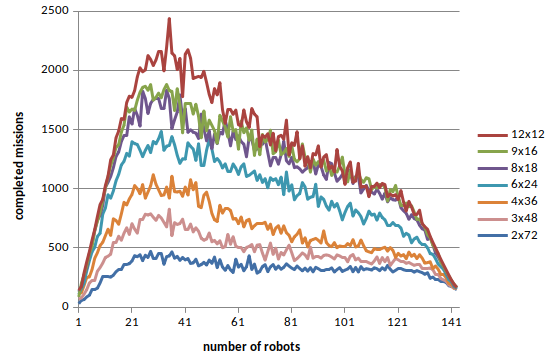
Using random cyclic task assignments, the next figure shows the number of completed missions versus number of robots for one hour of simulated time, 144 grid nodes and up to 143 robots. The legend indicates experiments for grids with different aspect ratios. The maximum number of completed tasks always occurs for around 30 robots independently of the grid aspect ratio. The simulations were run headless and no deadlocks or collisions occurred, that’s 1001 flawless simulations!